[i] Начальные сведения о помехозащищенном кодировании на основе кода Хэмминга
- К1986ВЕ8Т: (7,4) с битом чётности для задания режима работы;
- К1986ВЕ8Т, К1986ВК01GI: (7,4) с битом чётности для задания режимах запуска EXTBUS_CFG+JB или EXTBUS_CFG+JA;
- К1986ВЕ8Т, К1986ВК01GI: (72,64) для внутренней памяти и памяти на внешней шине.
В данной статье кратко рассмотрено помехозащищенное кодирование на основе кода Хэмминга 7,4.
Содержание
|
1. Общий алгоритм генерации ECC и коррекции ошибок на основе кода Хэмминга 2. Начальная информация о коррекции ошибок на основе кода Хэмминга 7,4 3. Программная генерация ECC |
1. Общий алгоритм генерации ECC и коррекции ошибок на основе кода Хэмминга
Общий алгоритм коррекции ошибок (ECC), основанный на коде Хэмминга, на примере операции записи/чтения в МК К1986ВЕ8Т/К1986ВК01GI:
1. Запись слова А:
-
Кодирование исходного слова А. На основании записываемых данных (для слов (72,64) также используется адрес) вычисляется проверочные (контрольные) биты ECC, которые передаются на запись совместно с исходным словом А.
-
Запись слова А вместе с контрольными битами ECC.
2. Чтение слова А:
-
Чтение слова А совместно с контрольными битами ECC.
-
На основании данных (для (72,64) данных и адреса) слова А производится повторный расчёт контрольных бит ECC.
-
Сравнение считанных проверочных бит ECC с заново рассчитанными. Если проверочные биты совпадают, значит ошибок нет, ECC биты отбрасываются и исходное слово А передаётся дальше на чтение.
-
Если проверочные биты не совпадают и имеет место одиночная ошибка, то происходит её исправление, операция чтения при этом также успешно выполняется. Если обнаружена двойная ошибка, то данные не восстанавливаются, и происходит ошибка чтения.
2. Начальная информация о коррекции ошибок на основе кода Хэмминга 7,4
В данном разделе рассмотрено построение кода Хэмминга 7,4, чтобы понять, как производится генерация ECC и коррекция одиночных ошибок.
Для обеспечения надёжной передачи данных в ненадёжном канале связи при кодировании на основе кода Хэмминга необходимо выполнение условия (1).
2k>=k+m+1, (1)
где m - длина исходного слова, k - длина контрольных бит.
Для надёжной передачи 4 бит информации (m), исходя из выше указанного неравенства (1), необходимо добавить к ним ещё 3 проверочных бита (k).
В обозначении 7,4 первое число (7) определяет количество бит закодированного слова, второе (4) - количество бит исходного слова.
Пусть имеется исходное слово A = (a3, a2, a1, a0). Для возможности исправить единичную ошибку с помощью кодирования Хэмминга необходимо вычислить контрольные биты ЕСС на основании исходного слова, которые будут передаваться совместно со словом А. Таким образом, в результате кодирования получится слово X = (r2, r1, r0, a3, a2, a1, a0), где r[2:0] - проверочные (контрольные) биты ECC.
Вычисление проверочных разрядов r[2:0] выполняется по формулам (2).
r2 = a3 ⊕ a2 ⊕ a1;
r1 = a3 ⊕ a2 ⊕ a0; (2)
r0 = a3 ⊕ a1 ⊕ a0;
⊕ - сложение по модулю 2.
Данные уравнения для проверочных бит подобраны таким образом, чтобы каждый проверочный бит r зависел сразу от нескольких бит a исходного слова. При этом изменение одного бита исходного слова вызовет изменение как минимум двух проверочных бит. По этим изменениям и определяется ошибка.
Для математического описания кодирования и декодирования исходных слов вводят специальные матрицы: матрицу G генерации и матрицу H проверки.
Матрица генерации G формирует закодированное слово путём перемножения слова A и матрицы генерации G, формула (3).
X = AG, (3)
операция суммирования производится по модулю 2.
Операция умножения матриц приведена на рисунке 1.
Рисунок 1 - Произведение матриц AB
При перемножении матриц для кодирования Хэмминга вместо «+» используется ⊕ (сложение по модулю 2).
Матрица G для кода 7,4 показана на рисунке 2.
Рисунок 2 - Матрица генерации G
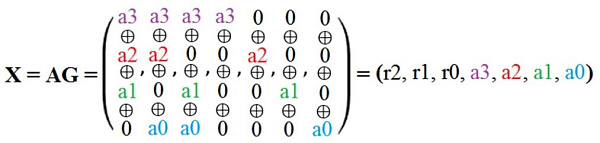
Произведение матриц AG приведено на рисунке 3.
Рисунок 3 - Произведение матриц AG
Таким образом, перемножив A и G, было получено закодированное слово X, состоящее из слова A и проверочных бит r[2:0].
При чтении закодированного слова X заново выполняется расчёт контрольных бит на основе слова А, а затем вычисленные и считанные контрольные биты складываются по модулю 2, формулы (4). Результат сложения образует так называемый синдром S = {S2, S1, S0}. По синдрому определяется ошибка, если таковая была.
S2 = r2 ⊕ r2' = r2 ⊕ a3 ⊕ a2 ⊕ a1;
S1 = r1 ⊕ r1' = r1 ⊕ a3 ⊕ a2 ⊕ a0; (4)
S0 = r0 ⊕ r0' = r0 ⊕ a3 ⊕ a1 ⊕ a0;
где r[2:0]' - заново вычисленные проверочные биты на основе считанного слова А.
Для расчёта синдрома S[2:0], аналогично матрицы генерации G, вводят проверочную матрицу H. Синдром формируется путём перемножения считанного слова X и транспонированной проверочной матрицы HT, формула (5).
S = X HT (5)
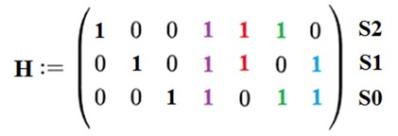
Проверочная матрица H для кода Хэмминга 7,4 имеет вид, показанный на рисунке 4.
Рисунок 4 - Проверочная матрица H
Каждая строка этой таблицы при побитом перемножении на слово X образует соответствующий бит синдрома.
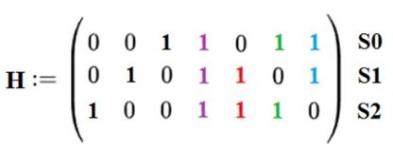
Если поменять местами строки 1 и 3, то получим проверочную матрицу, указанную в спецификации, при этом изменится порядок следования бит синдрома S = {S0, S1, S2} (рисунок 5).
Рисунок 5 - Проверочная матрица H из спецификации на МК К1986ВЕ8Т/К1986ВК01GI
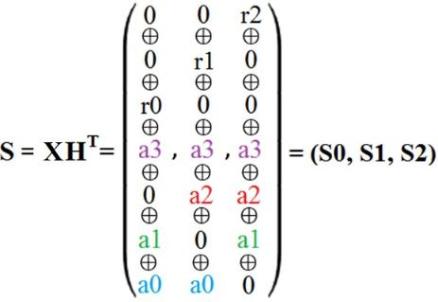
Операция перемножения X и HT (H матрица из спецификации) приведена на рисунке 6.
Рисунок 6 - Произведение матриц XHT
По получившемуся вектору синдрома и проверочной матрице H можно определить, где произошла ошибка. Если ошибки не было, то синдром равен 0: S = (0, 0, 0). Если же произошла одиночная ошибка, то совпадающий с синдромом столбец указывает на ошибочный бит (рисунок 7).
Рисунок 7 - Определение ошибки по проверочной матрице H с использованием синдрома S
Так, например, если синдром S = (0, 1, 0), значит, ошибка произошла в r1, если S = (0, 1, 1), то ошибка в a2. Определив по синдрому ошибочный бит, необходимо его инвертировать, чтобы восстановить исходное слово.
Чтобы этого избежать, вводят дополнительный бит четности p (parity), с помощью которого можно определить, произошла одиночная ошибка либо двойная и более. Тогда, если имеет место однократная ошибка, слово можно исправить, если двукратная - слово восстановлению не подлежит.
Бит чётности может занимать любую позицию в закодированном слове. В МК К1986ВЕ8Т/К1986ВК01GI бит четности расположен на 0 позиции проверочных бит, формула (6).
X = (r2, r1, r0, p, a3, a2, a1, a0) (6)
Бит чётности p вычисляется на основе всех остальных бит слова X путём их сложения по модулю 2, формула (7).
p = r2 ⊕ r1 ⊕ r0 ⊕ a3 ⊕ a2 ⊕ a1 ⊕ a0; (7)
При определении ошибки заново вычисляется бит чётности p' и складывается со считанным битом p, при этом данный результат будет являться новым битом синдрома. Так как бит чётности был добавлен на 0 позицию проверочных бит, то слово синдрома S = {S0, S1, S2, S3} приобретёт вид, как показано в формулах (8).
S0 = p ⊕ p' = p + r2 ⊕ r1 ⊕ r0 ⊕ a3 ⊕ a2 ⊕ a1 ⊕ a0;
S1 = r0 ⊕ r0' = r0 ⊕ a3 ⊕ a1 ⊕ a0;
S2 = r1 ⊕ r1' = r1 ⊕ a3 ⊕ a2 ⊕ a0; (8)
S3 = r2 ⊕ r2' = r2 ⊕ a3 ⊕ a2 ⊕ a1;
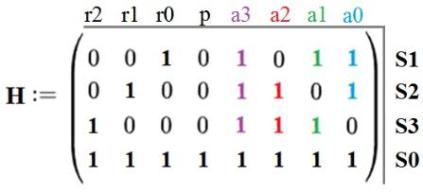
С учётом бита чётности проверочная матрица H будет иметь вид, показанный на рисунке 8.
Рисунок 8 - Проверочная матрица с учётом бита чётности
Как и в предыдущем случае, при возникновении одиночной ошибки позиция инвертированного бита определяется по совпадению синдрома и столбца проверочной матрицы (рисунок 9). Однако теперь, если значение синдрома не совпадает ни с одним из столбцов и не равно 0, значит, произошло более одной ошибки, и, следовательно, слово исправить нельзя.
Рисунок 9 - Определение ошибки по проверочной матрице H с использованием синдрома S
Для кода Хэмминга (72,64) генерации ECC и коррекция ошибок осуществляется точно таким же образом, но используемые матрицы больше. Надо заметить, что для кода (72, 64) расстояние Хэмминга позволяет определять двойные ошибки, а потому бит чётности в данном коде не используется.
3. Программная генерация ECC
В спецификации приведён пример программного вычисления проверочных бит ЕСС для кода Хэмминга (72, 64). Как уже было отмечено ранее, в данном коде не используется бит чётности, поэтому алгоритм вычисления ECC для кода (7,4) с битом чётности будет отличаться от алгоритма для кода (72,64). В связи с этим далее будет рассмотрена программная реализация вычисления ECC для кода (7,4) c битом чётности на примере вычисления бит CFGx в режимах запуска EXTBUS_CFG+JB и EXTBUS_CFG+JA.
Процесс вычисления проверочных бит заключается в перемножении исходного слова А и матрицы генерации ECC, которой является правая часть проверочной матрицы H. Код функции вычисления закодированного слова приведён во фрагменте кода 1.
Фрагмент кода 1 - Функция генерации закодированного слова на основе кода Хэмминга 7,4 с битом чётности
uint8_t Gen_ECC(uint8_t data)
{
uint8_t G[] = {0, 0xB,0xD,0xE}; // Матрица генерации
uint8_t i = 0, j = 0, res = 0, inputw = 0;
data = data & 0xF;
for (i=1; i<4; i++) { // Формирование r3-r1
inputw = data & G[i]; // Выбор необходимых информационных бит для формирования
// контрольного бита
res=0;
for (j=0; j<4; j++)
res = res ^ ((inputw >> j) & 0x01); // Суммирование выбранных информационных бит
// по модулю 2 для получения одного
// контрольного бита
data |= res<<(i+4); // Дописывание контрольных бит к исходному слову
}
res=0; // Формирование бита чётности p
for (j=0; j<8; j++)
res = res ^ ((data >> j) & 0x01); // Суммирование всех бит получившегося слова
// для нахождения бита чётности (S0)
return data |= res<<4;
}
В начале функции инициализируется массив генерации G[], при этом каждый элемент данного массива будет представлять строку правой части матрицы H. Далее в цикле формируются проверочные биты путем выборки необходимые информационных бит из исходного слова, а именно, накладывается маска из массива генерации, после чего они суммируются по модулю 2. Данный цикл выполняется для трёх проверочных бит, после чего полученные проверочные биты дописываются к информационным битам. Далее вычисляется бит чётности p путем суммирования по модулю 2 всех проверочных и информационных бит. Бит чётности также дописывается в кодируемое слово.
Получившиеся значения закодированного слова для всех исходных значений бит CFGx[3:0] приведены в таблице 1.
Таблица 1 - Исходные и закодированные слова на основе кода Хэмминга 7,4 с битом чётности
|
Закодированное слово |
Проверочные биты ECC |
Информационные биты CFGx |
|
0x00 |
0000 |
0000 |
|
0x71 |
0111 |
0001 |
|
0xB2 |
1011 |
0010 |
|
0xC3 |
1100 |
0011 |
|
0xD4 |
1101 |
0100 |
|
0xA5 |
1010 |
0101 |
|
0x66 |
0110 |
0110 |
|
0x17 |
0001 |
0111 |
|
0xE8 |
1110 |
1000 |
|
0x99 |
1001 |
1001 |
|
0x5A |
0101 |
1010 |
|
0x2B |
0010 |
1011 |
|
0x3C |
0011 |
1100 |
|
0x4D |
0100 |
1101 |
|
0x8E |
1000 |
1110 |
|
0xFF |
1111 |
1111 |
Сохранить статью в PDF